排序-快速排序

算法解析

快速排序算法有两个核心点，分别是 哨兵划分 和 递归

哨兵划分

以数组某个元素（一般选取首元素）为基准数，将所有小于基准数的元素移动到其左边，大于基准数的元素移动至其右边。
通过一轮哨兵划分，可将数组排序问题拆分为 两个较短数组的排序问题 （本文称之为左（右）子数组）。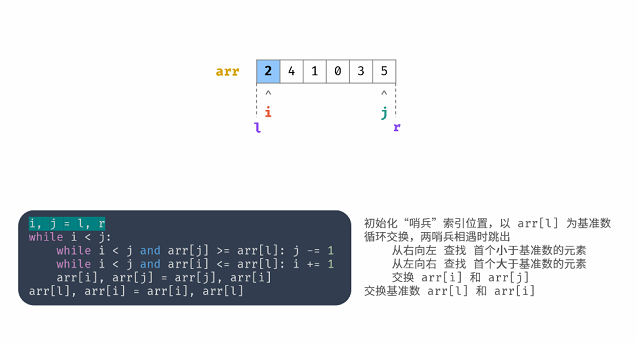

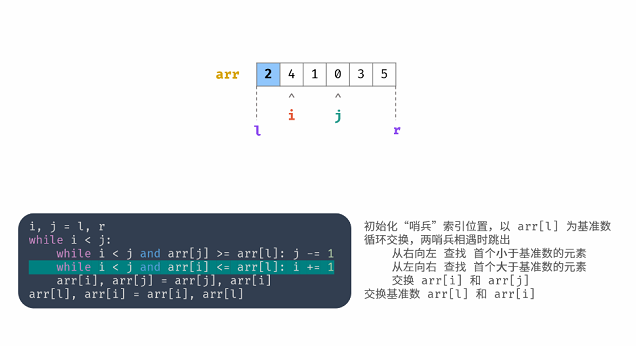
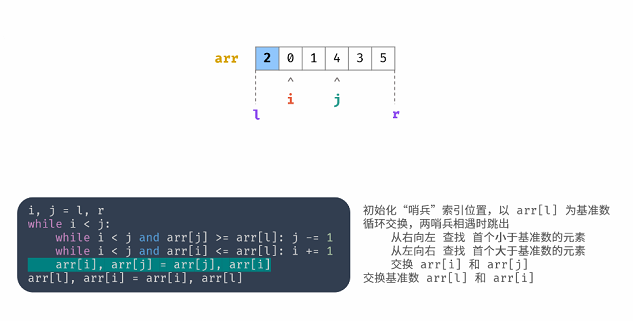
初始化“哨兵”索引位置，以arr[l]为基准数循环交换，两哨兵相遇时跳出
    从右向左 查找 首个小于基准数的元素
    从左向右 查找 首个大约基准数的元素
    交换 arr[i] 和 arr[j]
交换基准数 arr[l] 和 arr[i]

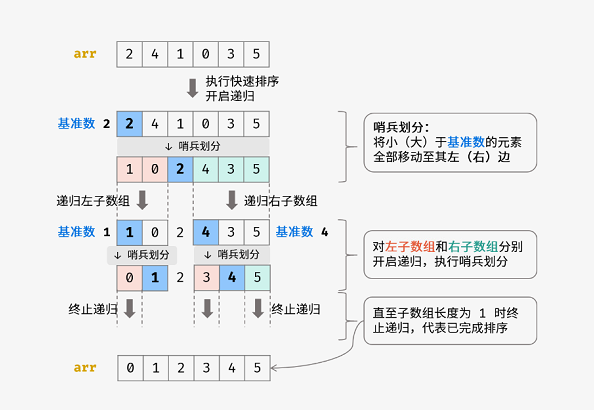
递归

对左子数组和右子数组分别递归执行哨兵划分，直至子数组长度为1时终止递归，即可完成对整个数组的排序

算法实现

import java.util.Arrays;

public class QuickSort {

    public static void quickSort(int[] nums, int l, int r) {
        if (l >= r) {
            return;
        }
        // 找到哨兵
        int i = partition(nums, l, r);
        // 递归左数组
        quickSort(nums, l, i - 1);
        // 递归右数组
        quickSort(nums, i + 1, r);
    }

    /**
     * 找哨兵
     *
     * @param nums
     * @param l
     * @param r
     * @return
     */
    public static int partition(int[] nums, int l, int r) {
        // 以nums[l]作为基准数
        int i = l, j = r;
        while (i < j) {
            // i为左，j为右
            // 从右向左找首个小于基准数l（i）的元素
            while (i < j && nums[j] >= nums[i]) {
                j--;
            }
            // 从左向右找首个大于基准数l（i）的元素
            while (i < j && nums[i] <= nums[j]) {
                i++;
            }
            // 开始交换
            swap(nums, i, j);
        }
        // 相等时，交换基准数与当前位置
        swap(nums, i, l);
        return i;
    }


    public static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    public static void main(String[] args) {
        int[] nums = {4, 1, 3, 2, 5};
        System.out.println("排序前：" + Arrays.toString(nums));
        quickSort(nums, 0, nums.length - 1);
        System.out.println("排序后：" + Arrays.toString(nums));
    }

}

参考文章

https://leetcode.cn/leetbook/read/grokking-algorithms/royq0v/